The winners of the 1st PACE competition were presented at ALGO 2016 in Aarhus. For those that couldn’t make it to Aarhus: here are the results. We would like to thank all participants for making this 1st edition of PACE an enjoyable and successful one.
Track A: Treewidth
The treewidth of a graph is an important graph parameter, the theory and complexity of which has been intensely study in graph minor theory and fixed-parameter tractability (FPT). Given a graph G and an integer k, it is NP-complete to determine whether the treewidth of G is at most k, but there is an n^(k+2)-time algorithm (Arnborg, Corneil, and Proskurowski 1987). The problem can also be solved in FPT-time exp(k^3) n (Bodlaender 1996), and a factor-5 approximation can be obtained in time exp(k) n (Bodlaender, Drange, Dregi, Fomin, Lokshtanov, and Pilipczuk 2013). It is unknown whether the problem has a polynomial-time approximation scheme (PTAS).
Treewidth implementations are used in various contexts. For example, compilers allocate registers by computing proper colorings on control flow graphs, which turn out to have small treewidth in practice (e.g., Thorup 1998). Data structures for shortest path queries can use tree decompositions in a preprocessing phase (e.g., Chatterjee, Ibsen-Jensen, and Pavlogiannis 2016). Graph theory can be guided by treewidth implementations when attempting to rigorously determine the treewidth of specific graph families (e.g., Kiyomi, Okamoto, and Otachi 2015). Finally, many problems in probabilistic inference use tree decompositions in a preprocessing phase (e.g., Otten, Ihler, Kask, and Dechter 2011).
While some treewidth implementations existed before PACE 2016, they were not easily accessible and sometimes buggy (as in the case of the Python SAGE implementation, which can produce non-optimal solutions), and their performances have never been compared in public. For PACE, we imposed a unified input/output format for the challenge and required all implementations to be made available on github. Moreover, the details and raw data of all results mentioned in this document can be found in the github repository [https://github.com/holgerdell/PACE-treewidth-testbed] that we published; using the tools and benchmark instances in the repository, it is a trivial matter to reproduce the results.
Submissions
The list of all implementation submissions can be found here: https://github.com/holgerdell/PACE-treewidth-testbed/blob/master/pace2016-submissions.yaml
Two people submitted real-world instances:
- Johannes Fichte (TU Wien) submitted transit networks.
- Ben Strasser (Karlsruhe Institute of Technology) submitted road graphs.
Exact treewidth
The goal of this challenge was to compute a tree decomposition of minimum width. Three teams participated in this track, and two PACE co-organizers contributed a further implementation.

This plot shows one data point per solver-instance pair. The x-coordinate corresponds to the treewidth of the instance and the y-coordinate corresponds to the running time. We aborted the computation after a timeout of 100 seconds for most instances; some instances had a timeout of 1000 and 3600 seconds; in total, we used 200 instances in the exact competition. The instances are samples of named graphs, control flow graphs, and DIMACS graph coloring instances.
Results and Techniques
- Tamaki (Meiji University) solved 199 instances. The submission is written in C++ and is based on a modified version of the brute force approach of Arnborg et al. (1987). [https://github.com/TCS-Meiji/treewidth-exact]
- Bodlaender & Van der Zanden (Utrecht University) solved 173 instances. The submission is written in C# / Mono and relies on balanced separators as well as dynamic programming. [https://github.com/TomvdZanden/BZTreewidth]
- Bannach, Berndt, Ehlers (Luebeck University) solved 166 instances. The submission is written in Java 8 and relies on a SAT-solver to find the optimal elimination order. [https://github.com/maxbannach/Jdrasil]
The Larisch & Salfelder (Frankfurt University) implementation solved 171 of 200 instances.
Heuristic treewidth
The goal of this challenge was to compute a good tree decomposition in a given fixed timeout. We set the timeout to 100 seconds for every instance. We used the 200 instances from the exact competition and 81 additional, harder instances from the same sources; arguably, the instances were generally too easy for the heuristic challenge. Seven teams participated in this track (9 sequential programs and 3 parallel programs were submitted). Some teams submitted multiple programs, in which case we only kept the best-performing submission of each team in the ranking.
Sequential programs
- Strasser (Karlsruhe Institute of Technology)
[https://github.com/ben-strasser/flow-cutter-pace16] - Fox-Epstein (Brown University)
[https://github.com/elitheeli/2016-pace-challenge] - Abseher, Musliu, Woltran (TU Wien)
https://github.com/mabseher/htd] - Gaspers, Gudmundsson, Jones, Mestre, Rümmele (UNSW and University of Sidney)
[https://github.com/mfjones/pace2016] - Bannach, Berndt, Ehlers (Luebeck University)
[https://github.com/maxbannach/Jdrasil] - Joglekar, Kamble, Pandian (IIT Madras)
[https://github.com/mrprajesh/pacechallenge]
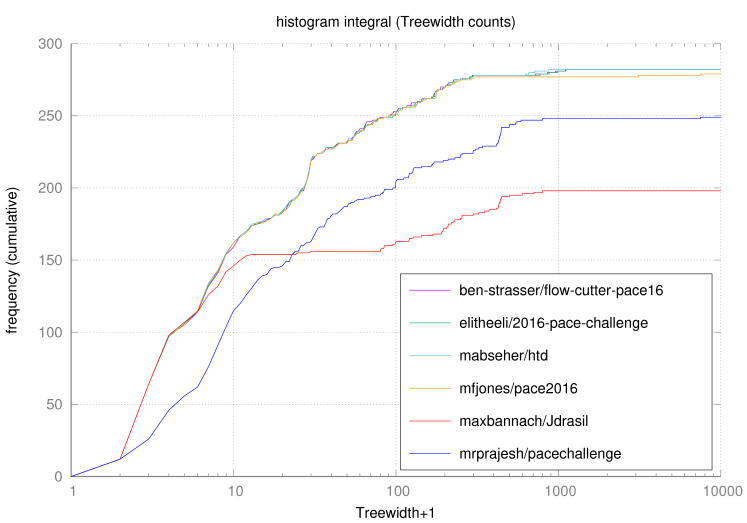
This plot shows, for every sequential submission and every x, the number y of instances for which the submission computed a tree decomposition of width at most x. As can be seen, the top three submissions nearly converge on this metric; this is perhaps explained by the fact that all three implement the basic MinFill heuristic (tweaked in different ways). The other three submissions use more interesting techniques from FPT.
For the evaluation, we viewed each instance as a voter and determined its ranking for the implementations from the width of the tree decomposition produced by the implementation after 100 seconds. We combined these votes using the Schulze method. This process can be inspected in the testbed repository [https://github.com/holgerdell/PACE-treewidth-testbed/blob/github/logs/2016-08-13.02-08-25/ranks-he-se.txt].
Parallel programs
- Kask, Lam (University of California at Irvine)
[https://github.com/willmlam/CVO2] - Strasser (Karlsruhe Institute of Technology)
[https://github.com/ben-strasser/flow-cutter-pace16] - Bannach, Berndt, Ehlers (Luebeck University)
[https://github.com/maxbannach/Jdrasil]
Track B: Feedback Vertex Set
In the Feedback Vertex Set problem we are given an undirected graph G and want to compute a smallest vertex set S such that removing S from G results in a forest, that is, a graph without any cycles. Feedback Vertex Set is NP-complete and one of the most prominent problems in parameterized algorithmics. Most fixed-parameter algorithms use the parameter solution size k=|S|.
Virtually all fixed-parameter algorithms make use of the fact that vertices of degree at most two can be easily removed from the graph. After this initial removal, a range of different techniques were used in the fixed-parameter algorithms. The first fixed-parameter algorithm branches on a shortest cycle in the resulting graph. This cycle has length O(log n) which results in an overall running time of k^k * poly(n). By using a randomized approach on the resulting graph, a running time of 4^k * poly(n) can be obtained. The first deterministic approaches to achieve running times of the form 2^O(k) * poly(n) use the iterative compression technique which iteratively builds up the graph by adding one vertex at a time and makes use of the fact that a size-k solution can be stored during this computation. Other fixed-parameter algorithms for this problem can be obtained by branching on a vertex of maximum degree or by LP-based techniques.
Challenge Setup and Participation
We collected 230 graphs which were mostly from various application fields such as social networks, biological networks, road networks, incidence graphs of CNF-SAT formules. The graphs were selected so that there was a steady progression from easy to hard instances.
To determine the winners, we counted the number of instances that could be solved within the given time limit. To avoid overemphasizing low-level improvements of the algorithms, we set the time limit to 30 minutes per instance. To identify programs that report nonoptimal solutions we precomputed the optimal solutions for some instances using an ILP that was given at least 30 minutes on each instance. This ILP is based on cycle constraints. More precisely, we add constraints enforcing that for each cycle at least one vertex must be deleted by any solution. Since the number of constraints is usually exponential, they are added in a lazy fashion, that is, we compute a solution with only some initial constraints and check whether the solution is a feedback vertex set. If this is the case, then we have found an optimal solution, otherwise we add constraints for some of the remaining cycles and compute a new solution until a feedback vertex set is found.
Overall, 14 teams registered out of which seven eventually submitted a program. From those teams that submitted a program, three were from Germany, one from India, one from Japan, one from Poland, and one from Russia.
Challenge Results
In the following, we give for each team further details such as the number of solved instances, a brief algorithm description, the names of the participants, and a link to the code repository. The entries are sorted by place in descending order. All submissions apply a reduction rule that removes all vertices of degree at most two.
- Yoichi Iwata (NII) and Kensuke Imanishi (University of Tokyo). This submission solved 84 out of 130 instances. The algorithm utilizes an LP-based branching and an LP-based kernelization. The program is written in Java and available at https://github.com/wata-orz/fvs.
- Marcin Pilipczuk (University of Warsaw). This submission solved 66 out of 130 instances. The algorithm branches on a vertex of maximum degree. In addition, instances with small treewidth are solved by dynamic programming on tree decompositions and subcubic instances are solved by a polynomial-time algorithm that is based on a reduction to the graphic matroid parity problem. The program is written in C++ and available at https://bitbucket.org/marcin_pilipczuk/fvs-pace-challenge.
- Ruben Becker, Karl Bringmann, Dennis Gross, Erik Jan van Leeuwen, and
Natalie Wirth (MPI Saarbrücken). This submission solved 50 out of 130 instances. The algorithm also branches on vertices of the highest degree, the search tree is pruned by computing upper and lower bounds. The program is written in C++ and available at https://github.com/erikjanvl/FVS_MPI. - Niklas Paulsen, Kevin Prohn, Malin Rau, and Lars Rohwedder (Kiel University). This submission solved 47 out of 130 instances. The algorithm is based on the combination of iterative compression with an improved branching strategy. Subcubic graphs are solved again by reduction graphic matroid parity. The program is written in C# and available at https://git.informatik.uni-kiel.de/npau/FFF.
- Shivam Garg (IIT Bombay), G. Philip and Apoorva Tamaskar (Chennai Mathematical Institute). This submission solved 41 out of 130 instances. The algorithm branches on a shortest cycle. This program is written in Python and available at https://bitbucket.org/gphilip_bitbucket/pace-code.
- Fabian Brand, Simon Gehring, Florian Nelles, Kevin Wilkinghoff, and Xianghui Zhong (University of Bonn). This submission solved 34 out of 130 instances. The algorithm is based on iterative compression and also solves subcubic instances in polynomial time. The program is written in C++ and available at https://github.com/s-gehring/feedback-vertex-set.
- Svyatoslav Feldsherov (Moscow State University). This submission solved 22 out of 130 instances. The algorithm uses the randomized approach with running time 4^k n^O(1). An improvement is gained for the case where two vertices are connected by a multiedge. In this case, the algorithm branches directly on these two vertices. The program is written in C++ and available at https://github.com/feldsherov/pace2016.
As a final remark, the ILP solved 81 out of 130 instances. Thus, the best FPT approaches were competitive with this particular ILP formulation. Since better ILP formulations are possible, a more thorough comparison with further ILP-based approaches would be necessary to gain insight into the relative performance of FPT-based and ILP-based approaches for Feedback Vertex Set.
I just stumbled across this – really interesting stuff.
With respect to the Feedback Vertex Set challenge, is there anywhere that I can download the ILP formulation that was used as a comparator?
LikeLike